図1. GigaSt・スペアナのブロック構成図のページを見る
(GigaSt 青山さんのご厚意により block.gifの画像を転載しております)
まず、ブロック図(図1)の左上から見ていきましょう。ここで、[1G-IN」、[2G-IN]とありますが、これは測定する信号の周波数帯域別により、入力方法・ユニットの接続構成が異なることを意味しています。
すなわち[1G-IN」は、センター周波数が1000MHz未満の時で、3MHz〜1200MHzまでのLOW-BANDの入力範囲になっています。一方[2G-IN]は、センター周波数が1000MHz以上の時で、950MHz〜2150MHzまでのHIGHT-BANDの入力範囲としています。ここで、[2G-IN]を選択した場合には、1Gユニットと2Gユニット間は接続せず、[2G-IN]に直接信号を入れることになります(このとき1Gユニットは関係しない)。
バンドの切り替えは、同軸コネクタの接続を切り替えることで行っています。もし、センター周波数が1GHz以上の時で、間違えて信号を[1G-IN」に入力してしまった場合には、1300MHzを中心としたイメージが発生してしまいます。イメージ信号を本来あるべき信号として間違えてしまわないように、接続・設定には注意してください。
スペアナの基本動作原理で述べたように、ミキサーの特性は、実際には式(2)で表されますが、N=1,M=1とした理想的な場合として、式(1)のみを考えてみます。ミキサーの入出力周波数の関係式は、
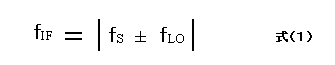 |
ここで式(1)は、3つのパターンに分けられます。すなわち、2つの入力として、入力信号 fs と局部発振器信号 fLO から、
(A) fIF=fs+fLO
(B) fIF=fs−fLO ただし、 fs > fLO のとき
(C) fIF=fLO−fs ただし、 fLO > fs のとき
となります。
さて、1Gユニットは、LOW-BAND(3MHz〜1200MHz)の信号を観測するときに使いますが、分かり易く考えていけるように、これから具体的な数値を用いてみます。
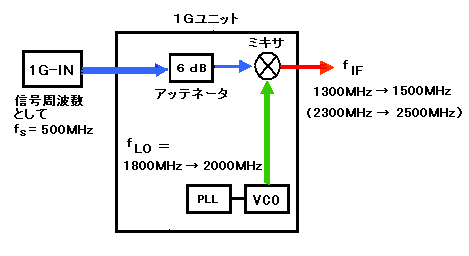 |
| 図2. 1Gユニットのブロック図と入出力関係 |
1Gユニットのブロック図(図2)ではVCOとありますが、これが電圧制御発振器で、スペアナの基本動作原理図から見ると掃引局部発振器に相当します。また、PLLとありますが、これはVCOを正確かつ安定な周波数で掃引させる回路です。
さて、VCOの掃引周波数 fLOは1400MHzから2600MHzまで可変することができますが、センター周波数の設定とスパンの設定により、可変する周波数幅が決められます。ここでは、センター周波数を500MHz、スパンを200MHzに設定したとします。測定周波数範囲(もしくは表示周波数範囲) fsは400MHzから600MHzまでの200MHz幅なのですが、掃引周波数 fLOは、1800MHzから2000MHzまでの200MHz幅となります。すなわち、測定周波数範囲(表示周波数範囲) fs と掃引周波数範囲 fLO との関係は、式1(C)の fIF=fLO−fsで、fIF=1400MHzとの関係になっています。
例えば、fs=500MHzの信号が、[1G-IN]に入力されるというように想定してみます。 ミキサーの入出力周波数の関係式として、式1(C)を用いると、
fs=500MHz、fLO=1900MHz、fIF=1400MHzとなります。この場合のスペクトラムの位置関係を、図3(LO固定時)に示します。
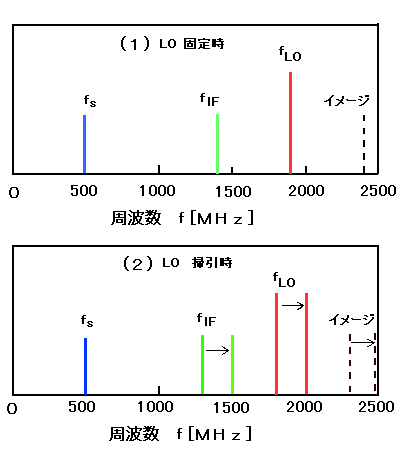 |
| 図3. ミキサーの入出力周波数 (Lo固定時と掃引時の場合) |
ところで、ミキサーの入出力の関係は、他に式1(A) fIF=fs+fLO もあります。すなわち、fIF=2400MHzのところにイメージが発生します。
実際には、fIF=2400MHzのところに発生したイメージは、次の段に接続されている2Gユニット内のBPF(バンドパスフィルタ)で除去され、fIF=1400MHzのIF信号のみが通過できるように構成されています。
さて、次に信号 fs は、500MHzのままで、局部発振器の信号 fLO をPLLにより1800MHzから2000MHzまでの200MHz幅で掃引する場合を考えます。このとき、式1(C)の関係式から、図3(LO固定時)に示すように、IF出力 fIF は1300MHzから1500MHzまで変化します。
一方、イメージ周波数については、式1(A)より、2300MHzから2500MHzまでの範囲で発生しますが、BPFで除去されます。
ところで、局部発振器 fLO は掃引を周期的に繰り返すようにPLLで設定されています。このとき1掃引に要する時間、すなわち測定の周期を例えば10秒(注)として考えてみます。
(注) 実際には、パソコンのスピードやサンプリング回数により1掃引時間は変わりますが、1000MHzのスパンのとき目安として次のような感じです。スパンが狭くなればサンプリング回数が少なくてもよいため、さらに時間は短くなります。
75MHz CPU------ 10秒
200MHz CPU------ 4秒
366MHz CPU------ 3秒
図4は、1掃引に要する時間(測定周期)を10秒として、横軸に時間 t[s]、縦軸に周波数fをとってミキサーーの入出力周波数と時間の関係を示したものです。
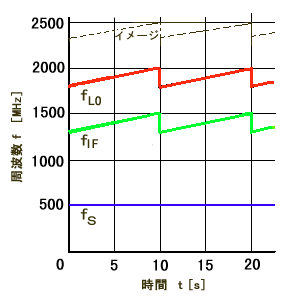 |
| 図4. LO掃引時のミキサー入出力周波数の変化 |
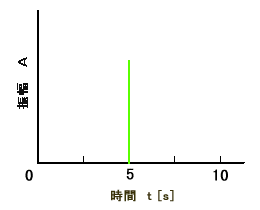 |
| 図5. LO掃引時の表示 |
入力に信号を入れていなくとも、センター周波数が0MHzで大きなピークが見られます。Giga-Site・スペアナで実際の観測データ例を掲載します。
入力に信号を入れていないのに、ピークが発生しているのは、なぜか?
と思われている人もいると思います。これは、明らかにイメージです。発生のメカニズムは、式(1)からわかると思います。
fs=0MHzとして見てください。fIF=fLO となります。すなわち、局部発振器の周波数 fLOが、IF周波数となってしまっています。fs =0MHzのピークは、実は局部発振器の周波数によるイメージだったのです。
式(1)をもう一度、見てみましょう。
(A) fIF=fs+fLO
(B) fIF=fs−fLO ただし、 fs > fLO のとき
(C) fIF=fLO−fs ただし、 fLO > fs のとき
復習になりますが、入力信号(観測したい周波数)を、fs=500MHzとしたとき、1Gユニットの局部発振器の掃引周波数は、fLO=1900MHzで、fIF=1400MHzとなります。すなわち、式1(C)が入出力の関係式になっていました。一方、式1(A)では、fLO=1900MHzで、fIF=2400MHzとなるイメージですが、このfIF=2400MHzの周波数はIFフィルタで除去できるものです。
さて、それでは式1(B)の場合はどう考えられるでしょうか。1Gユニットは、LOW-BAND(3MHz〜1200MHz)の信号を観測するときに使いますが、もし、fs=500MHzの信号を観測しているときに、1Gユニットの入力に、fs=2400MHzの入力信号が入ったとしたら、どうでしょうか。
(C)式より fs=500MHzの信号が、fIF=1400MHzとなり、一方、(B)式より fs=2400MHzの入力信号が fIF=1400MHzになってしまいます。この場合の表示画面では、500MHz本来の信号のピークなのか、2400MHzの信号のピークなのか区別できなくなります。
500MHzの信号がなくとも、2400MHzの信号が入れば、500MHzのところにあたかも信号があるように見えてしまうため、2400MHzの信号によるイメージということになります。
この場合には、1Gユニットの入力にLPF(ローパスフィルタ)を取り付け、2400MHzが入力に入らないようにすると防ぐことができます。
各ユニットの前段には、アッテネータが挿入されています。アッテネータの役割は、高周波信号のレベル調整[ブロック図で、ATTと記載]と、もう一つは整合改善[ブロック図で、6dBと記載]の2つの役割を持っていると思います。ここでは、整合の改善について解説します。
アッテネータは高周波回路にとって必要不可欠なもので、スペアナに限らず、標準信号発生器、電界強度計、RFミリボルト計などに必ず用いられています。
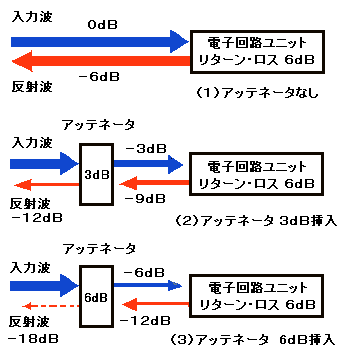 |
| 図7. アッテネータの挿入による整合改善 |
図7は、アッテネータの挿入による整合改善の例です。入力のリターン・ロスが6dBである整合があまりとれていない電子回路ユニットがあるとします。
図7(1)は、アッテネータがない場合で、電子回路ユニットに信号を入力すると、6dB減衰するものの反射波として入力端に戻ってきてしまいます。
ここで、(2)のように入力端に3dBのアッテネータを入れると、反射波は、12dBも減衰してくれます。すなわち、アッテネータで往復3dB、帰路3dB、合計6dB減衰し、電子回路ユニットの入力リターン・ロスが6dBであるため、トータルのリターン・ロスは、12dBとなるのです。
さらに、(3)のように入力端に6dBのアッテネータを入れると、さらに反射波は−18dBとなります。このように、アッテネータを入れることにより、整合が大幅に改善できることがわかります。
[次へ]は、GigaStスペアナの詳細、第2段です。
 |
|
 |
|